Análise combinatória é uma matéria que costuma causar certo medo nos alunos. Então, se você está lendo este blog post, eu já te parabenizo por enfrentar o medo e encarar a matéria de frente! 

via GIPHY

Então, vamos lá: para te ajudar a estudar análise combinatória para o Enem, vamos primeiro falar sobre PFC. E não, não estamos falando sobre o Premier Futebol Clube, mas sobre o Princípio Fundamental da Contagem. 

Princípio Fundamental da Contagem: o raciocínio por trás da análise combinatória

O princípio fundamental da contagem diz que se um acontecimento é formado por duas etapas independentes e sucessivas uma da outra, pode-se afirmar 2 coisas:

1 – A 1ª etapa pode acontecer de N modos;

2 – Para cada um desses modos, a 2ª etapa pode ocorrer de m modos. Então, o número de possibilidades de ocorrência do acontecimento pode ser n . m ou n + m. Em outras palavras, podemos usar o princípio aditivo ou o princípio multiplicativo. 

Se a questão envolve: 

OU> utiliza-se + > princípio aditivo

E > utiliza-se . > princípio multiplicativo

É sempre assim: se a analise combinatória usou OU, somamos as possibilidades. Sempre que usar E, multiplicamos as possibilidades.

Isso muitas vezes não aparece claro na questão, você tem que analisar a situação.Então, vamos a um exemplo:

Imagina que existam 3 cidades, X Y e Z. Quero saber de quantas maneiras posso ir de X a Z. Primeiramente, olhando pra figura, existe maneira de sair direto e ir de x a z sem passar pelo Y? Existe, então posso ir direto. Mas não é a única chance, posso ir direto OU ir de X a Y e ir de Y a Z. Então quantas possibilidades de caminho eu tenho pra ir de X a Z? Duas possibilidades. De x a Y? 3 possibilidades. De Y a Z? 2 possibilidades. 

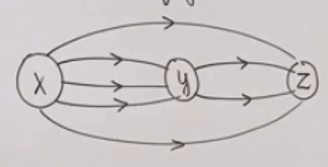
Agora vamos aplicar o princípio multiplicativo e aditivo. Porque posso ir direto de X a Z ou posso passar por Y. Então, fica: 

X > Z    OU  X > Y    E  Y > Z. 

2             +     3        x        2

2             +               6 

            =  8

 

Por princípio de matemática básica, sabemos que primeiro resolvemos a multiplicação. Então, temos que o resultado são 8 maneiras diferentes de ir de X até Z. Mas essa questão são poucos caminhos, podemos tirar a prova e contar no desenho, utilizando as setas desenhadas. Normalmente, as respostas são números grandes, por isso é importante que você fixe o conceito de princípio aditivo e multiplicativo. 

Agora, imagine a seguinte questão: 

Considere os algarismos 1, 2, 3 e 4. Quantos números com algarismos distintos são maiores que 300?

Primeiro raciocínio: esse número pode ter 3 algarismos? Pode! E ele também pode ter 4 algarismos. Então, temos que ele pode ser:

_ _ _ OU _ _ _ _ 

Eu sei que isso parece muito básico, mas é necessário fixar esse início, que é o princípio da análise combinatória. Ou seja: ele é determinante pra sua compreensão da matéria. 

Continuando: a questão determina que uma condição é que os números sejam maiores que 300. 

Vamos trabalhar, primeiro, com a possibilidade de um número com três algarismos. Logo, o 1º algarismo só pode ser 3 ou 4, ou seja, temos duas possibilidades. O 2º algarismo pode ser três possibilidades (pois não pode ser algarismos repetidos). No 3º e último algarismo, restam duas possibilidades. Utilizaremos o princípio multiplicativo, ficando assim:

Passamos, agora, para a possibilidade do número de 4 algarismos. Nesta opção, podemos ter qualquer número no 1º algarismo, então são 4 possibilidades. Depois, excluindo esse, tem-se três possibilidades para o 2º algarismo, duas possibilidades para o 3º algarismo, e uma possibilidade para o último algarismo. Logo, a nossa resolução ficou assim:

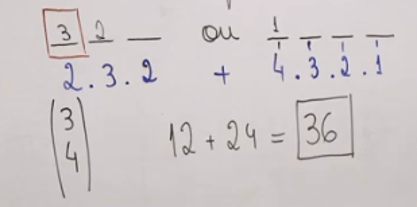
Somando, encontramos 36 possibilidades, ao todo. Isso porque o número pode ter três ou quatro algarismos. Logo, usamos o princípio aditivo. 

Pronto, exercício de análise combinatória resolvido! Mas é preciso que você entenda que cada exercício exige uma leitura da situação e do que é pedido. Portanto, cada questão te cobrará um raciocínio diferente. Entretanto, todos te exigirão pensar: “quem pode entrar, e quem não pode entrar”. Por isso, é primordial que você treine fazendo exercícios. A minha dica de como estudar análise combinatória, depois que você entendeu os princípios básicos, é essa: pratique fazendo exercícios.  

Para te ajudar, deixo aqui uma aula de explicação da matéria de análise combinatória, em que faço esse e outros exercícios. Depois dela, tenho certeza que você conseguirá resolver questões de anos anteriores do Enem! Assista: 

Se tiver alguma dúvida, comente aí embaixo. Nossa equipe do Matemática Online pode te ajudar!